 Chapter 5 of the Outline of basic music theory – by Oscar van Dillen ©2011-2020
Chapter 5 of the Outline of basic music theory – by Oscar van Dillen ©2011-2020
The beginner’s learning book can be found at Basic elements of music theory.
Overview of chapters:
Chapter 1: Introduction
Chapter 2: Sound and hearing
Chapter 3: Musical notation
Chapter 4: Basic building blocks of melody and harmony
Chapter 5: Consonance and dissonance
Chapter 6: Circle of fifths and transposition
Chapter 7: Concerning rhythm, melody, harmony and form
Chapter 8: Further study
Definitions of consonance and dissonance
Consonant literally means: sounding together
Dissonant literally means: sounding apart
Let us stop a moment and consider these concepts more closely. Especially the concept dissonant may seem strange in the context of music, which after all consists of sounds combined together into one piece. When playing simultaneous sounds, these will “sound together” by the very definition of their simultaneousness. The whole purpose of introducing the concepts of consonance and dissonance however, is to make distinctions in the nature and quality of the innummerable possibilities of combining sounds. But then, why just make this distinction seemingly oversimple and merely dual, almost resembling the opposites “good” vs “bad”?1
The quality of the “sound together” is in fact strongly depending on the musically formal and harmonical contexts in which it occurs. Correspondingly, according to Louis & Thuilles “Harmonielehre” one should distinguish between the phenomena of acoustic dissonance and interpretational dissonance (German: Auffassungsdissonant)2 I consider this phenomenon as an integral part of the concept of harmony in a wider sense, and distinguish further between formally and harmonically contextual dissonances.
Before going into finer detail, we shall consider the traditional classical theoretical view on consonance versus dissonance first.
Traditional classification of intervals in consonant and dissonant
Traditionally, only the basic the intervals are classified, based on their use in the type of harmony used in classical music.

This classification, though all too often still taught as factual, is actually rather outdated and of little practical value for most contemporary music, such as Jazz, Pop and World music, as well as contemporary composition; hence we will take a closer look at their actual acoustic properties next.
Acoustic order of consonance and dissonance in intervals
A tentative attempt has been made here to establish an acoustic order of the basic and wide intervals, starting with the most consonant, gradually evolving to the more dissonant, somewhat like Hindemith’s Reihe 23. In this order it can be observed how the wide intervals are in fact found in perhaps unexpected places for the traditionally educated music theoreticians, but as “the proof of the pudding is in the eating”, in sound “the proof of the theory is in the hearing”, as one can observe oneself.

This order may be true for these intervals exactly as notated, on c one octave below central c, and yet it may differ somewhat when gradually transposed to other tones, more so even in different registers. Also, this order can basically be regarded to be true for the instrument on which it is perceived, here: the piano. But consonance and dissonance depend on the harmonics-structure of the instrument used, as well as on the medium for the sound waves: the air itself, so far taken for granted. Dolphins, porpoises and whales, living in and using an enormous variety of sounds under water, in many more octaves than we humans can perceive, should have a quite different perception of these intervals. Good examples of completely different sets of intervals in world music are offered by Indonesian gamelan: the bells used produce totally different overtones than the piano.
 When composing, arranging or improvising, great care has to be taken to judge the sounds intended not on mere theoretical grounds, but on the actual perception intended, clearly and precisely defined, taking exact register positions into account, or else one may end up with music that looks good (on paper), but sounds bad, as is all too often the case when relying too much on general theoretical knowledge, superficially studied, only partly digested and not fully understood.4
When composing, arranging or improvising, great care has to be taken to judge the sounds intended not on mere theoretical grounds, but on the actual perception intended, clearly and precisely defined, taking exact register positions into account, or else one may end up with music that looks good (on paper), but sounds bad, as is all too often the case when relying too much on general theoretical knowledge, superficially studied, only partly digested and not fully understood.4
Consonance and dissonance in scales
Consonance and dissonance in scales is generated from the presence and position of contextual harmonically dissonant intervals embedded within a particular scale. Thus all diatonic scales contain at least one tritone, and most pentatonic scales have no dissonant intervals at all.
Dissonance in a scale adds a harmonic element of tension to its melodic structure, certain tones always stand out in a particular scale, exactly because of this.
Let us consider this in the church modes.
The most remarkable tones by which we recognize the church modes are:
- the sharp 4 in lydian
- the flat 7 in mixolydian
- the natural 6 in dorian
- the flat 2 in phrygian
- the flat 5 in locrian
Which does make one wonder about the two remaining modes: by what special characteristics do we recognize ionian and aeolian, also known as the basic major and minor scales, or do they stand out in a negative sense, by having no special characteristics at all?5
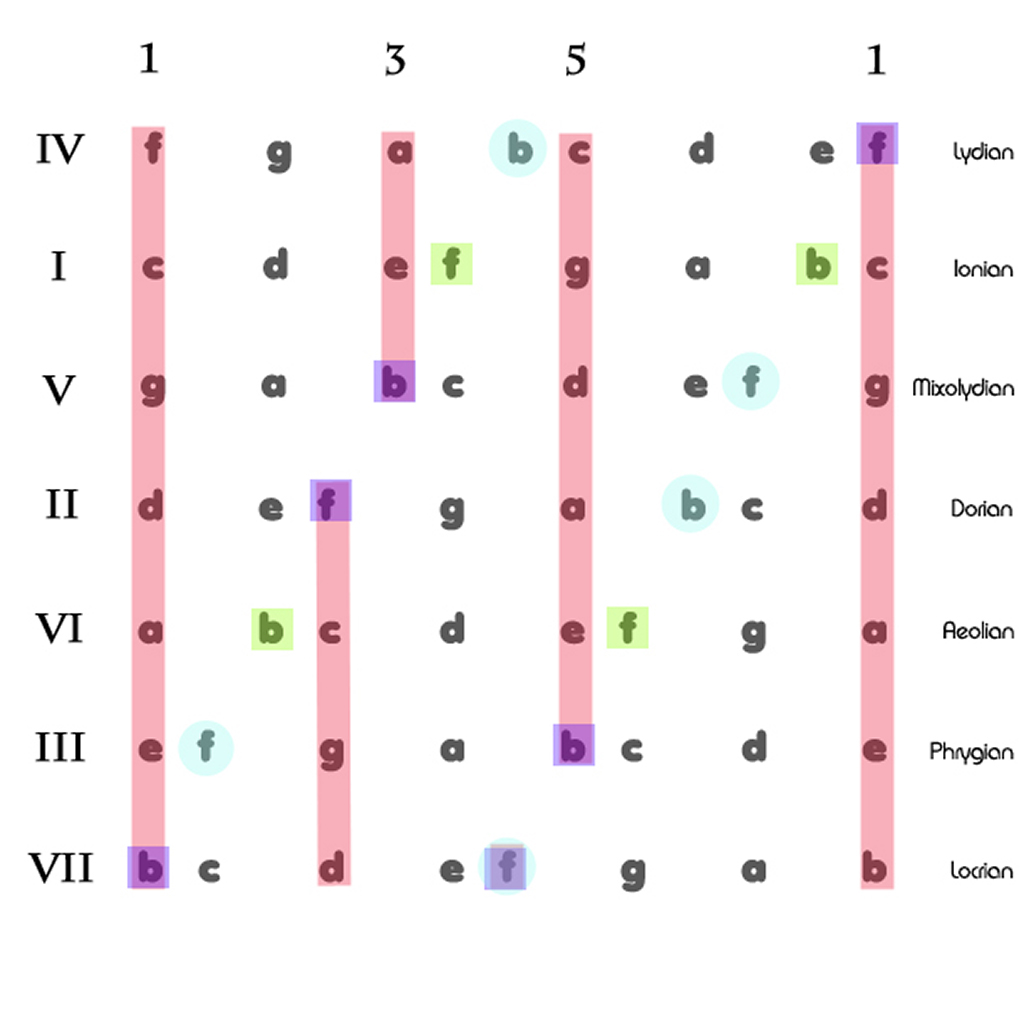 Now, as the image presented here attempts to show:
Now, as the image presented here attempts to show:
- all remarkable tones are part of an embedded tritone;
- in all 5 remarkable cases this tritone is connected to the basic triad 1-3-5 supporting the scale, the remarkable tone being outside the triad on 2, 4, 6 or 7 (except in locrian which has the tritone on 1-5);
- only in ionian (4-7) and aeolian (2-6) the complete embedded tritone is disconnected from this basic triad.
So we can conclude that the major and natural minor scales are well suited for tonal music, which depends on the use of triads 1-3-5 throughout, as the tritones embedded in these scales do not burden its basic sound with dissonance, reserving its embedded tension to be used on degrees other than its proper tonic I.
The accuracy of this phenomenological observation and line of reasoning are strongly confirmed by the fact that for tonal use, the minor harmonic scale is customary, which does not flatten the 7th tone, and which like natural minor has a tritone between 2 and 6. In this scale a second tritone is introduced by the natural 7, adding more tension to this scale. The position of this additional tritone now is remarkably enough between 4 and 7: exactly the same as in ionian (major). Therefore we can conclude that by embedding both tritones the minor harmonic scale combines the tension properties of major and minor into one scale, which sheds quite a new light on the concepts of molldur and durmoll, which are customary in functional harmony.6
Finally, this procedure gives some clues as to how one can go about harmonizing makams and ragas, and in fact to the different phenomenology of harmony itself in music based on modes such as these, many of which are not harmonically connected to 3 and 5 by their performance traditions.
Traditional classification of chords in consonant and dissonant
Traditionally, only chords with perfect fifths between 1 and 5, and in the case of seventh chords also between 3 and 7, are considered consonant.
 Noteworthy is that the second inversion of the consonant chords is considered to be a typical contextual dissonant.
Noteworthy is that the second inversion of the consonant chords is considered to be a typical contextual dissonant.
Use of consonance and dissonance
Consonance is a term that describes the phenomenon of several sounds or pitches blending together, almost as if becoming one, a unity of sound. Dissonance on the other hand, is a term that describes tension in sound, as if sounds or pitches do not blend together, and remain separate auditive entities. The apperception of whether sounds do or do not blend is highly subjective however, and strongly dependent on musical context, whereas tension is a more objectively measurable property in sound itself.
In functional harmony, that is: harmony employing degrees and thus harmonic functions, the usual order is that of an increase of tension followed by a moment relaxation, so using more and increasing dissonance, sometimes with the use of non-harmonic tones7 to be followed and the tension released by consonance. The consonance is always chosen in relation to the musical context, the dissonants employed are style- and context-related as well. As a general rule however, it is the dissonants which represent the strongest expressional means in harmony.
Oscar van Dillen ©2011-2020
goto chapter 6 ► Circle of fifths and transposition
Footnotes
- A similar simplified “interpretational truth” usually arises from the famous medieval quote “Tritonus Diabolum in Musica est” (the tritone is the devil in music) which does not mean the tritone sounds bad nor that it is bad, but that one has to be extra careful handling, using, this particular interval. Thus a rather non-condemning uncontemporary medieval practical mind speaks from these words in fact. In the centuries after, the tritone, as we now know, developed its full potential as the basis of all functional harmony, even though most musical theoretical models rather stuck to the much simpler perfect fourths and fifths (“Quintfall”, falling fifth or circle progression) or even seconds (“Sekundgang”, stepwise progression) for their ultimate explanations. One might however conclude that the tritone’s primal harmonic potential was suspected and perceived much earlier by musicians, and at the time certainly not regarded as an enemy of the earlier polyphony. ↩
- “Die Auffassung des vorhaltartigen (auffassungsdissonanten) Quartsextaccords als einer Harmonie, die sich nach dem Dominantaccord aufzulösen hat, ist uns freilich so sehr in Fleisch und Blut übergegangen, daß die Anwendung des betonten Quartsextaccords über einer andern als der 5. Stufe stets eine gewisse Vorsicht erheischt. Unser Ohr ist geneigt, die Stufe, auf der ein derartiger Quartsextaccord erscheint, als Dominante zu hören, bezw. wenn sie es nicht ist, dazu zu machen” (Louis & Thuille, Harmonielehre, Chapter II §16(49), page 57). ↩
- Paul Hindemith, Unterweisung im Tonsatz (1937), Section 3 ↩
- Recommended further reading on this is Morton Feldman, ”Essays” (1985); a lengthy talk in 2 parts on these and other matters concerning music by Morton Feldman is available at the Internet Archive at archive.org ↩
- An interesting comparison in this case is Tanya Khovanova’s puzzle “Which is the odd one out?” at blog.tanyakhovanova.com ↩
- Have these questions been raised before, have they been answered? As far as I know, these seemingly obvious facts and observations have been overlooked by theoreticians for centuries, and have by my knowledge never been published before. ↩
- see kaitlinbove.com for more details and types ↩
