 Chapter 6 of the Outline of basic music theory – by Oscar van Dillen ©2011-2020
Chapter 6 of the Outline of basic music theory – by Oscar van Dillen ©2011-2020
The beginner’s learning book can be found at Basic elements of music theory.
Overview of chapters:
Chapter 1: Introduction
Chapter 2: Sound and hearing
Chapter 3: Musical notation
Chapter 4: Basic building blocks of melody and harmony
Chapter 5: Consonance and dissonance
Chapter 6: Circle of fifths and transposition
Chapter 7: Concerning rhythm, melody, harmony and form
Chapter 8: Further study
Circle of fifths
Major scales in order of accidentals
It is possible to construct a major scale on every tone, and different accidentals are needed to induce the proper order of steps: whole, whole, half in both tetrachords (4 tone scale part). Without use of accidentals, only the scale of c major yields this strucure in both tetrachords: both c d e f and g a b c share this structure: 1 1 ½. These tetrachords are both connected to the fundamental c, the first has it as lowest, the second as highest note. The remaining interval f g is a consequence of this tetrachordal construction, and in itself a whole step (major second). The total scale thus shows 1 1 ½ 1 1 1 ½.
When constructing this on different tones, we can set the scales we find into the following order by number of accidentals, those we find having sharps:
 And those we find having flats:
And those we find having flats: If we allow for the use of double sharps and flats, more scales are possible, but for practical reasons the keys (and hence the scales) remain limited to those employing a maximum of 7 accidentals.
If we allow for the use of double sharps and flats, more scales are possible, but for practical reasons the keys (and hence the scales) remain limited to those employing a maximum of 7 accidentals.
Minor scales in order of accidentals
It is also possible to construct a similar series when studying minor. In order to obtain similar accidentals, we use the minor-parallel or parallel minor scale, or aeolian mode, which can be found on the VI of any major scale. VI of c being the a we find the following order by number of accidentals, with sharps: And another series yet, employing flats instead, starting with the parallel of f, d:
And another series yet, employing flats instead, starting with the parallel of f, d:
Key signatures in order of accidentals
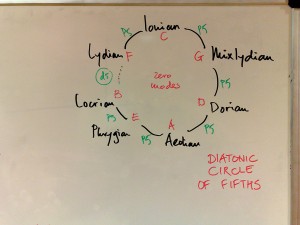 Note that both orders are based upon the diatonical series of fifths we discovered earlier:
Note that both orders are based upon the diatonical series of fifths we discovered earlier:
either, for the sharps
- f c g d a e b
or the reverse, for the flats
- b e a d g c f
which form a diatonic circle of fifths, as shown again in this image, that also mentions the church modes. Not all these fifths are perfect however, this diatonic circle of fifths contains one diminished fifth: f – b.
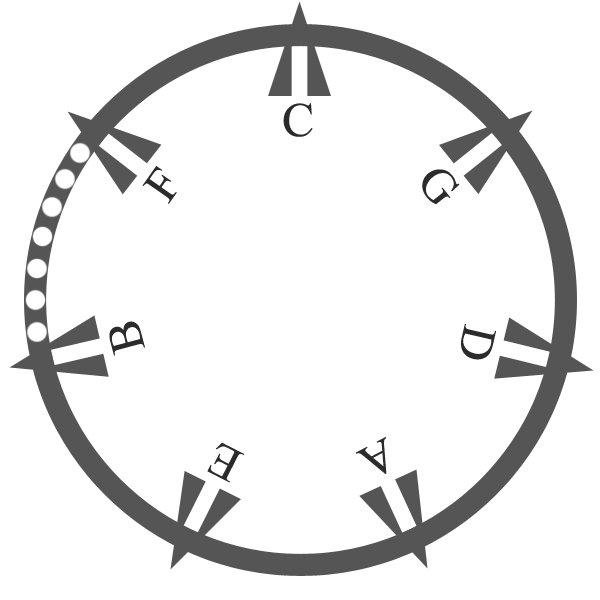
Diatonic circle of fifths
The order of appearance of sharps is fixed as:
f# → c# → g# → d# → a# → e# → b#
the example shows the correction notation of the key-signatures with sharps on two clefs: The order of appearance of flats is also fixed and the exact reverse as to the use of basic tones:
The order of appearance of flats is also fixed and the exact reverse as to the use of basic tones:
b♭ → e♭ → a♭ → d♭ → g♭ → c♭ → f♭
the example shows the correction notation of the key-signatures with flats on two clefs:
Geometry of the full circle of fifths
We can now summarize this structure and knowledge in the circle of fifths.
The image of the circle of fifths summarizes and visually represents the observations on major and minor scales and keys and the key signatures with number and order of sharps and flats, but it also allows a further geometrical look into the intervals, and their place within this representation.
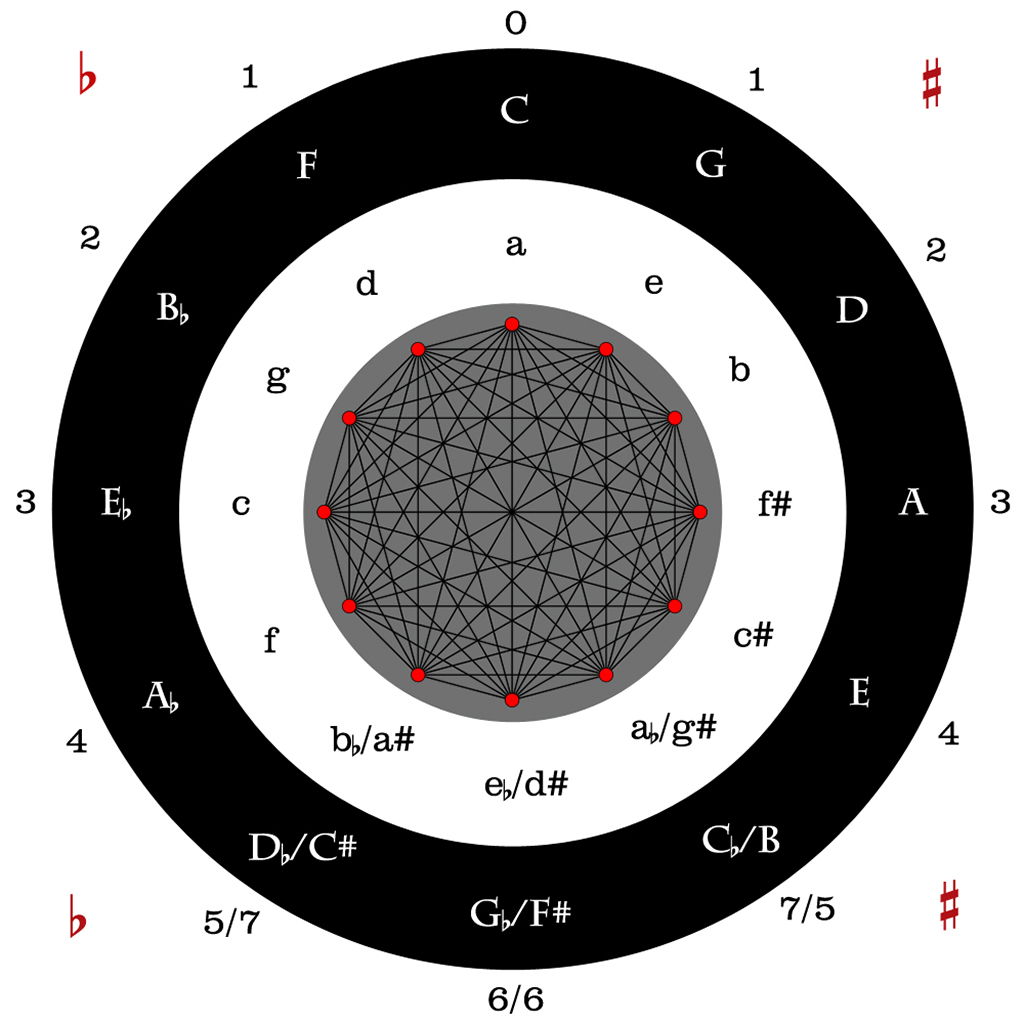 Here are some relevant observations which help in understanding and memorizing this visual representation of “musical geometry”:
Here are some relevant observations which help in understanding and memorizing this visual representation of “musical geometry”:
- There are the enharmonic equivalences of the major keys C♭=B (7 flats equals 5 sharps enharmonically), G♭=F# (6 flats equals 6 sharps enharmonically), D♭=C# (5 flats equals 7 sharps enharmonically);
- There are the enharmonic equivalences of the minor keys a♭=g# (7 flats equals 5 sharps enharmonically), e♭=d# (6 flats equals 6 sharps enharmonically), and b♭=a# (5 flats equals 7 sharps enharmonically);
- The enharmonic equivalences are true for the tempered tuning system alone, but this is the contemporary tuning system which we actually use in this basic music theory;
- The circle of fifths is not valid in other tuning systems;
- In the outer black ring the major keys are represented in white capitals;
- In the inner white ring the minor keys are represented in black minuscules;
- In the inner gray circle all possible interconnections between points are shown, these represent intervals;
- Outside the rings, the number of accidentals is shown, from zero up to seven;
- On the top and bottom left and right are red accidentals, to show the left side contains flats, and the right side contains sharps;
- The fact that the starting point C – a is represented on top, is arbitrary but customary;
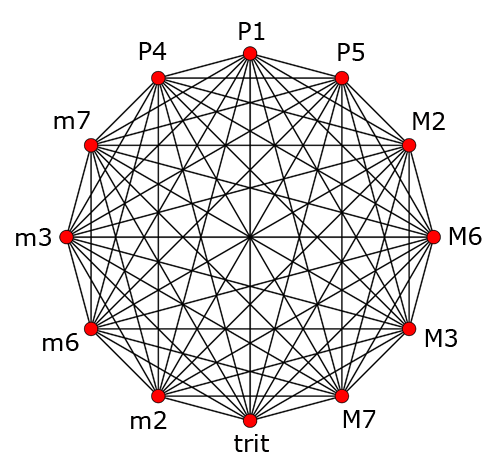
- Intervals can also be visualized in this geometrical representation, as the innermost gray circle contains all interconnections between all 2 points, these represent the following intervals (12-17):
- neighbours are a perfect fifth (or its inversion the perfect fourth) apart – completing this as a pattern one gets a dodecagon or the full circle of fifths;
- neighbours to neighbours, skipping one in between, are a major second apart (or its inversion the minor seventh) – completing this as a pattern one gets a hexagon or half the circle as a whole tone scale (acoustically there are only two such scales);
- skipping two one finds a minor third (or its inversion the major sixth) – completing this as a pattern one gets a square or a diminished seventh chord (acoustically there are only 3 such chords);
- skipping three one finds a major third (or its inversion the minor sixth) – completing this as a pattern one gets an equilateral triangle or an augmented triad (acoustically there are only 4 such triads);
- opposites are in a ”tritone” (augmented fourth or its inversion diminished fifth) relationship (acoustically there are only 6 such intervals);
- neigbours to opposites are a minor second apart (or its inversion the major seventh) – completing this as a pattern one gets the full circle as a 12 pointed star representing the chromatic scale (acoustically there is only 1 such scale);
- A still fuller circle of fifths is possible when wrapping the full sequence of flats, naturals and sharps of basic tones in order onto itself, 21 tones wrapped in the form of a 12 tone circle, with only g, d and a having no enharmonic equivalents with a single accidental: f♭ – c♭ – g♭ – d♭ – a♭ – e♭ – b♭ – f – c – g – d – a – e – b – f# – c# – g# – d# – a# – e# – b# where all fifths are perfect. Doing this however would lead to needlessly encumbering the image with highly unusual keys and scales, as well as to overflooding the eye with too much information, but one can and should attempt to imagine this overcomplete image nevertheless.
Circle of fifths as interval calculator
The circle of fifths can also be used as an interval calculator, as shown below:
Circle of fifths as interval calculator
The Spiral of fifths and the Pythagorean comma
The whiteboard below shows the gradual development of the circle of fifths out of a series of basic tones, curled onto itself as a spiral:
- step 0: Original ancient deduction of basic tones from a as μεσος1 using perfect fifths, creating pentatonic and diatonic scales, finding the tritone;
- step 1: Diatonic circle of fifths, also the basis for the order of sharps and flats;
- step 2: Diatonic spiral of fifths, charting all flat and sharp alterations of basic tones;
- step 3: Chromatic spiral of fifths including Pythagorean comma,2 a dilemma for tuning;
- step 4: Full chromatic circle of fifths with major and minor keys and geometry of intervals.
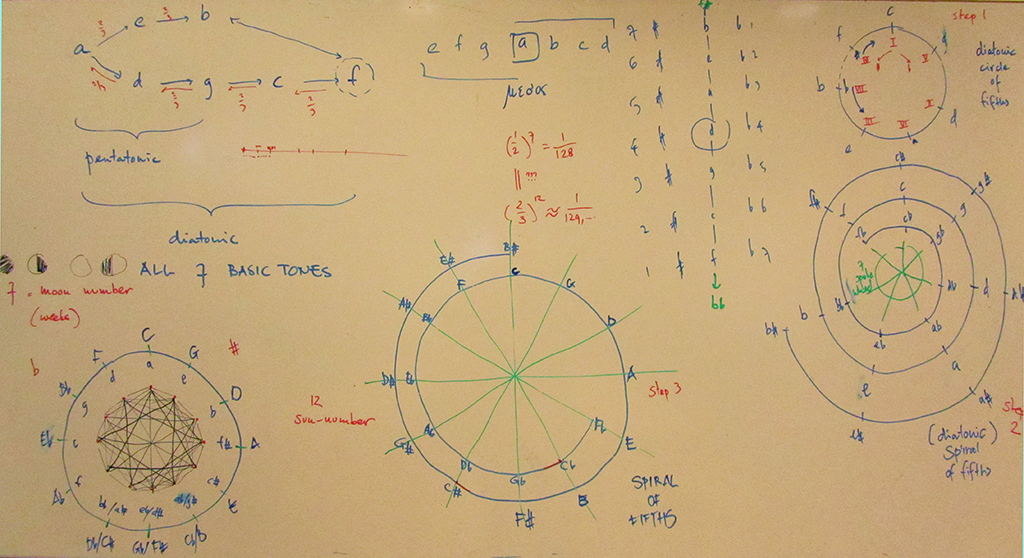 Making sure to check and gradually understand fully all of these steps towards, and observations on, the circle of fifths, will enable one to memorize it as more than a mere photographic image, but rather as a dynamic “Gestalt” or “Mandala”, implied by and underlying the tone-structure of the tempered tuning system.
Making sure to check and gradually understand fully all of these steps towards, and observations on, the circle of fifths, will enable one to memorize it as more than a mere photographic image, but rather as a dynamic “Gestalt” or “Mandala”, implied by and underlying the tone-structure of the tempered tuning system.
Map of keys

1817 Map of keys by Gottfried Weber
Gottfried Weber was the first to formulate a map of keys in 1817, defining four relationships to neighboring keys to any major key, leading to a 2-dimensional map of all keys:
- dominant relationship: perfect fifth up; one sharp added or one flat removed
- subdominant relationship: perfect fifth down, one sharp removed or one flat added
- major to relative (sometimes also known as parallel) minor: same key signature, tonic minor third down
- major to parallel (sometimes also known as equal) minor key: same tonic but in minor
Mind that in the original image, H stands for B and B stands for Bb (German nomenclature).
Below is shown the basic principle of the map of keys, rotated clockwise by 90°; horizontal lines are circles of fifths; minor keys are represented by minuscules.
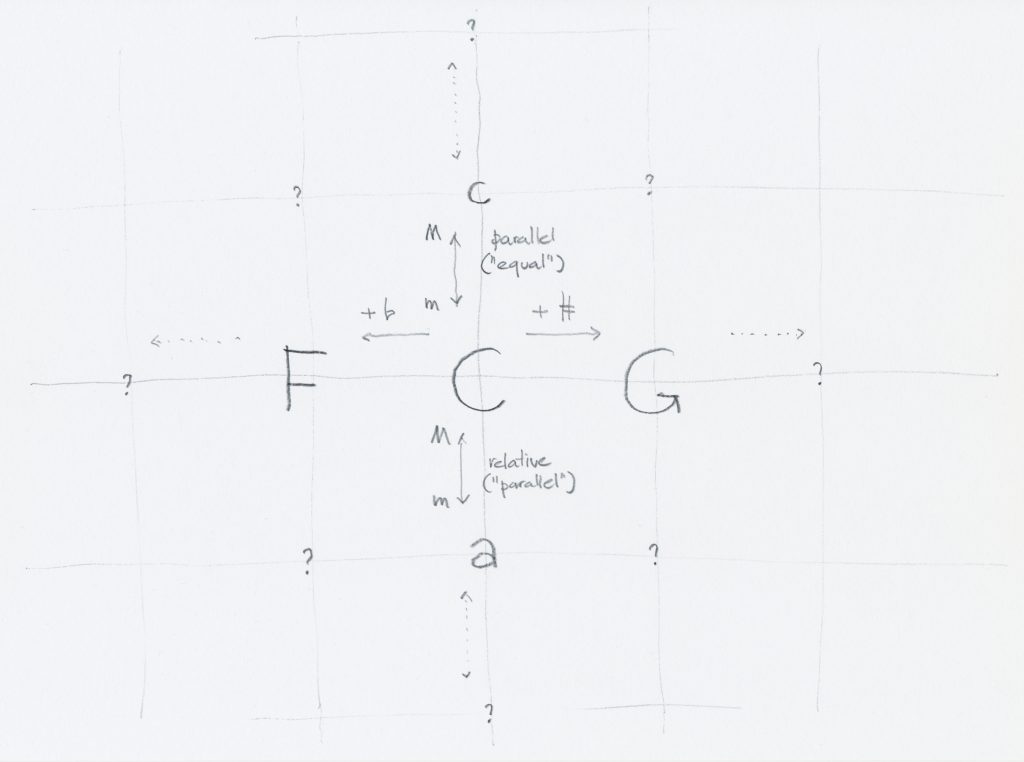
Basic principle of the map of keys
Additional notes on intonation and tuning systems
Here is a modest list of external links on the topic:
- Just intonation explained by Kyle Gann (website including audio examples for the intonations)
- Logarithms and musical intervals by Wright (pdf)
- A non-Pythagorean musical scale based on logarithms by Robert P. Schneider (pdf)
- Calculating with tones, the logarithmic of music by Klaus Kühn and Robert Shepherd (book)
- Scale Workshop, by Lumi Pakkanen, Sevish, Vincenzo Sicurella, Lajos Mészáros and Forrest Cahoon (interactive website with many resources)
Transposition
Definition of transposition
Transposition is the shifting of musical notation by a certain specific interval.
Use of transposition
Transposition may be used in order for a certain musical instrument to play the correct tones, or to change the key of a composition, song, or part of any music.
Commonly occurring reasons to transpose music are:
- to correctly write the staff or part for a transposing musical instrument3
- to fit the music to the ambitus (range) of a particular instrument
- to fit the music to the range of a particular singer or voice
- to change the key of a (part of a) piece of music
Example of transposition
The example below gives a melody in c then transposed for four different transposing instruments.
Please note that, when performed, all these different notations give the exact same pitches!
In C
This is an example of a melody, written “in C“, meaning the pitches sound exactly as notated, in the exact register as notated:

Soprano saxophone in B♭
As this instrument sounds a major second lower than notated, the music should now be transposed a major second up, not just the notes, but also the key signature:

Alto saxophone in E♭
As this instrument sounds a major sixth lower than notated, the music should now be transposed a major sixth up, not just the notes, but also the key signature:

Tenor Saxophone in B♭
As this instrument sounds a major ninth lower than notated, the music should now be transposed a major ninth up, not just the notes, but also the key signature:
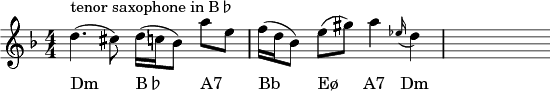
Baritone saxophone in E♭
As this instrument sounds a major thirteenth lower than notated, the music should now be transposed a major thirteenth up, not just the notes, but also the key signature:
 A special and unique peculiarity occurs with transposing for a baritone saxophone: the noteheads happen to be on exactly the same positions on the staff when written in either clef, sounding in f-clef or transposed in g-clef the positions are identical and only the alterations differ.
A special and unique peculiarity occurs with transposing for a baritone saxophone: the noteheads happen to be on exactly the same positions on the staff when written in either clef, sounding in f-clef or transposed in g-clef the positions are identical and only the alterations differ.
Most commonly occurring transposing instruments
This list is far from being exhaustive, see the footnotes for a link to a more complete list.
Woodwinds
- Flutes: Flauto d ‘Amore in Bb or A, Alto flute in G
- Oboes: English horn in F, Oboe d’Amore in A
- Clarinets: Piccolo clarinet in Eb and D, Clarinet in Bb and A, Basset horn in F, Alto clarinet in Eb, Bass clarinet in Bb
Brass instruments
- French horn in F (in older scores French horns in all transpositions can occur)
- Trumpet in Bb, Piccolo trumpet in D, Cornet in Bb, Flugelhorn in Bb
Saxophones
- Soprano saxophone in Bb
- Alto saxophone in Eb
- Tenor saxophone in Bb
- Baritone saxophone in Eb
Oscar van Dillen ©2011-2020
goto chapter 7 ► Concerning rhythm, melody, harmony and form
Footnotes
- μεσος (mesos) means “middle (tone)”: the ancient Greeks eventually constructed scales from a middle tone outwards, in two interlinked tetrachords. The modern concept of a fundamental tone came more than 2000 years later when functional harmony developed. ↩
- The Pythagorean comma is represented by this inequality:
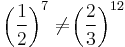 which is a calculation that refers to a tuning problem, and its provisionary solution is actually represented in the circle of fifths. In this formula and the following formulae, 1/2 is used instead of 2 throughout, representing the octave upwards instead of downwards (halving the ratio, as opposed to doubling), which may seem less customary but which does not change the logic nor the basic conclusions. The fractions represent the intervals of an octave (1/2) and a fifth (2/3), whereas the powers 7 and 12 are consecutive repetitions of these intervals. The formula can therefore be expressed in langague: “Seven octaves do not equal twelve fifths”. However, in the circle of fiths, in modern tempered tuning, they do equal one another! All the intervals are actually detuned to make this true, meaning that all the fifths commonly used are not truly perfect to nature, not exactly 2/3. The bridging of this “system-gap” of the Pythagorean comma is mathematically done by drawing upon a logarithmically calculated minor second, or semitone:
which is a calculation that refers to a tuning problem, and its provisionary solution is actually represented in the circle of fifths. In this formula and the following formulae, 1/2 is used instead of 2 throughout, representing the octave upwards instead of downwards (halving the ratio, as opposed to doubling), which may seem less customary but which does not change the logic nor the basic conclusions. The fractions represent the intervals of an octave (1/2) and a fifth (2/3), whereas the powers 7 and 12 are consecutive repetitions of these intervals. The formula can therefore be expressed in langague: “Seven octaves do not equal twelve fifths”. However, in the circle of fiths, in modern tempered tuning, they do equal one another! All the intervals are actually detuned to make this true, meaning that all the fifths commonly used are not truly perfect to nature, not exactly 2/3. The bridging of this “system-gap” of the Pythagorean comma is mathematically done by drawing upon a logarithmically calculated minor second, or semitone: 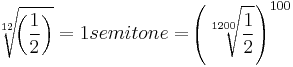 Today this is often represented in cents, a finetuning unit dividing the octave in 1200 steps:
Today this is often represented in cents, a finetuning unit dividing the octave in 1200 steps: 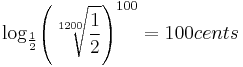 and so the exact interval can be calculated which, when repeated 12 times, equals 1 octave:
and so the exact interval can be calculated which, when repeated 12 times, equals 1 octave: In practice, this logarithmically regular scale, although significantly and hence audibly deviating from the Pythagorean sounds of the intervals, nevertheless leads to a currently acceptable spreading of a detuning over all the intervals, except the octave. The results are visualized in the diagram below, which sums up the Pythagorean and Tempered tuning pitches, and shows their differences:
In practice, this logarithmically regular scale, although significantly and hence audibly deviating from the Pythagorean sounds of the intervals, nevertheless leads to a currently acceptable spreading of a detuning over all the intervals, except the octave. The results are visualized in the diagram below, which sums up the Pythagorean and Tempered tuning pitches, and shows their differences: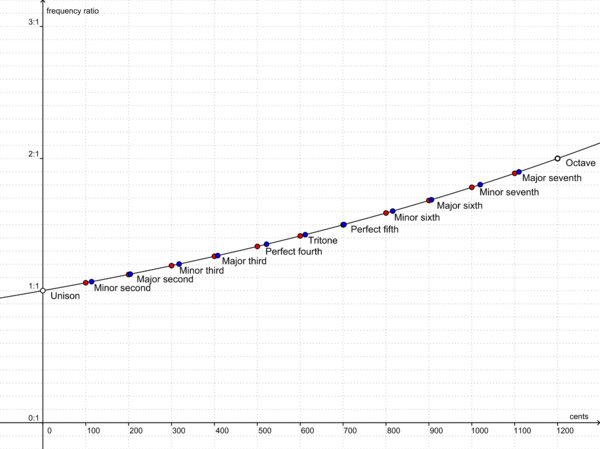 In this diagram it can clearly be seen which intervals differ most from their Pythagorean or natural versions (not all Pythagorean intervals should be considered to be simply “natural intervals” as well). Yet even this practical solution to the tuning problem is still really only strictly mathematically true, because on pianos (and modern keyboards) also and even the octaves are detuned, deliberately very slightly sharp, called stretched tuning, so as to bring out the diferent registers more clearly. Modern keyboards allow for custom tunings, to be programmed in cents; in this way players can customize their sounds all the way into the very intervallic fabric of their performance. On other musical instruments, the precise intonation is done by the musicians by more traditional techniques, and of course by their extremely acute hearing. In the end, for all musical instruments, what is actually played exactly, is (pre)determined by the (hopefully expert) ears. ↩
In this diagram it can clearly be seen which intervals differ most from their Pythagorean or natural versions (not all Pythagorean intervals should be considered to be simply “natural intervals” as well). Yet even this practical solution to the tuning problem is still really only strictly mathematically true, because on pianos (and modern keyboards) also and even the octaves are detuned, deliberately very slightly sharp, called stretched tuning, so as to bring out the diferent registers more clearly. Modern keyboards allow for custom tunings, to be programmed in cents; in this way players can customize their sounds all the way into the very intervallic fabric of their performance. On other musical instruments, the precise intonation is done by the musicians by more traditional techniques, and of course by their extremely acute hearing. In the end, for all musical instruments, what is actually played exactly, is (pre)determined by the (hopefully expert) ears. ↩ - List of transposing instruments on Wikipedia ↩
