Professional preparatory music theory: Basic elements of music theory.
Chapter 3 of the Basic elements of music theory – by Oscar van Dillen ©2014-16
The advanced learning book can be found at Outline of basic music theory.
Pages and chapters:
Chapter 1: Introduction
Chapter 2: Musical notation
Chapter 3: Building blocks of harmony – Scales
Chapter 4: Building blocks of harmony – Intervals
Chapter 5: Building blocks of harmony – Chords
Chapter 6: Keys and key signatures
Chapter 7: Further study
Building blocks of harmony
- Harmony consists of tones sounding together in time.
There are two types of sounding together in music: simultaneous and sequential. The musical sounding together can be accomplished by both means, and both can be included in the broad concept: harmony.
Building blocks of harmony – part 1: Scales
Scales
- A scale is a set of 5 or more tones, arranged in stepwise order, spanning an octave.
The simplest way to order a set of tones is in a scale. There exist a vast number of scales, but for the purposes of this elementary course this wealth is limited to a few, to be known really well for a start.
A scale arranges tones in a stepwise order. There are different kinds of steps, varying in size, the most common we will encounter are:
- the semitone step, abbreviated by the number ½
- the whole tone step, abbreviated by a number 1
- the next larger step of 1½, either by skipping a tone or by an altered neighboring tone
Steps and scales are different in different tuning systems, this course uses the equal tempered tuning throughout. The equal tempered tuning is today used for almost all Jazz- and Pop- and most World and Classical music. Other tunings are used in World music and so-called authentic performances of Baroque, Renaissance and Medieval music. The modern equal tempered tuning has as its huge advantage that all similar steps are equal:
- In equal tempered tuning all semitone steps are the same.
Pentatonic scales
With the material of the seven basic tones we can build the two most common pentatonic scales. The prefix penta comes from ancient Greek music theory, and means five, so: 5-tone scales. First let’s look at and listen to the major pentatonic scale of c, after listening you should sing it as well:

example 7 – pentatonic major scale
- the major pentatonic scale has 5 tones (here: c, d, e, g and a)
- the major pentatonic scale has the following structure of 5 steps: 1 – 1 – 1½ – 1 – 1½
Taking the exact same tone material, but now from a to a, we get the minor pentatonic scale of a, after listening to both these scales, practice singing them along and alone as well, keeping them well apart:

example 8 – pentatonic minor scale
- the minor pentatonic scale has 5 tones (here: a, c, d, e, and g)
- the minor pentatonic scale has the following structure of 5 steps: 1½ – 1 – 1 – 1½ – 1
You may have noticed that I have used both the terms “major pentatonic” and “pentatonic major”, and that these mean the exact same. Just the word “pentatonic” however denotes merely the 5-tone structure but does not make clear which pentatonic scale is meant.
EXERCISES 5
- Sing both these pentatonic scales on the same beginning tone;
- Figure out how to write both these pentatonic scales, beginning on the other 6 basic tones.
Basic diatonic scales
The basic diatonic scales are also known by their traditional name: church modes. The definition of a diatonic scale is that it consists of only whole and half steps, nothing larger therefore. The basic diatonic scales are also called modes, which can be a more complex concept as well. In practice the word mode is often used as meaning scale, but the word mode can be used to indicate a certain use of the scale as well.
The material for the basic diatonic scales, are the seven basic tones c, d, e, f, g, a and b. Arranging these in stepwise order, spanning an octave we get 7 scales, each with its traditional name, The student is advised to become fully familiar with these scales, and singing after hearing as well as singing along is a good start, noting its overall sound (mode), the different steps, and the detailed harmonic positions of the tones compared to its fundamental tone:

example 9 – ionian
- the ionian scale or mode is also known as the major scale, and one of the 3 basic major modes
- the step structure is 1 – 1 – ½ – 1 – 1 – 1 – ½
- this downwards step order is identical to the upwards step order of phrygian
- the harmonic positions of the tones are 1 – 2 – 3 – 4 – 5 – 6 – 7
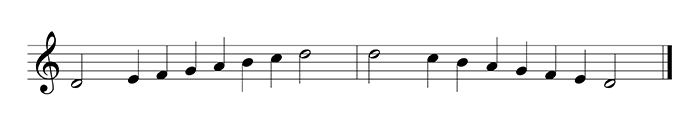
example 10 – dorian
- the dorian scale or mode is one of the 3 basic minor modes
- the step structure is 1 – ½ – 1 – 1 – 1 – ½ – 1
- this step structure is uniquely symmetrical: upwards and downwards gives the same order
- the harmonic positions of the tones are 1 – 2 – ♭3 – 4 – 5 – 6 – ♭7

example 11 – phrygian
- the phrygian scale or mode is one of the 3 basic minor modes
- the step structure is ½ – 1 – 1 – 1 – ½ – 1 – 1
- this downwards step order is identical to the upwards step order of ionian
- the harmonic positions of the tones are 1 – ♭2 – ♭3 – 4 – 5 – ♭6 – ♭7

example 12 – lydian
- the lydian scale or mode is one of the 3 basic major modes
- the step structure is 1 – 1 – 1 – ½ – 1 – 1 – ½
- this downwards step order is identical to the upwards step order of locrian
- the harmonic positions of the tones are 1 – 2 – 3 – ♯4 – 5 – 6 – 7

example 13 – mixolydian
- the mixolydian scale or mode is one of the 3 basic major modes
- the step structure is 1 – 1 – ½ – 1 – 1 – ½ – 1
- this downwards step order is identical to the upwards step order of aeolian
- the harmonic positions of the tones are 1 – 2 – 3 – 4 – 5 – 6 – ♭7

example 14 – aeolian
- the aeolian scale or mode is also known as natural minor scale, and one of the 3 basic minor modes
- the step structure is 1 – ½ – 1 – 1 – ½ – 1 – 1
- this downwards step order is identical to the upwards step order of mixolydian
- the harmonic positions of the tones are 1 – 2 – ♭3 – 4 – 5 – ♭6 – ♭7

example 15 – locrian
- the locrian scale or mode is the only diminished scale of the basic minor modes
- the step structure is ½ – 1 – 1 – ½ – 1 – 1 – 1
- this downwards step order is identical to the upwards step order of lydian
- the harmonic positions of the tones are 1 – ♭2 – ♭3 – 4 – ♭5 – ♭6 – ♭7
Especially the harmonic properties is important to consider: the question “which steps are in the scale” can be answered in two ways: the order and the harmonic positions. Both were provided in the bullets below each of the examples above. To show the harmonic positions more clearly, the table below is provided, where the scales can be read horizontally, and their basic tones seen vertically, as compared to the overall semitone scale of positions of the degrees 1, 2, 3, 4, 5, 6, and 7:
| 1 | ♭2 | 2 | ♭3 | 3 | 4 | ♯4♭5 | 5 | ♭6 | 6 | ♭7 | 7 | 8 | |
| lydian | f | g | a | b | c | d | e | f | |||||
| ionian | c | d | e | f | g | a | b | c | |||||
| mixolydian | g | a | b | c | d | e | f | g | |||||
| dorian | d | e | f | g | a | b | c | d | |||||
| aeolian | a | b | c | d | e | f | g | a | |||||
| phrygian | e | f | g | a | b | c | d | e | |||||
| locrian | b | c | d | e | f | g | a | b |
In this table the scales are presented by a harmonic order: first the 3 major scales, then the 3 minor scales and finally the diminished locrian scale. After having studied this table closely, you are ready for the following observations concerning harmony:
- a degree is a numbered step of a scale
- a major mode is characterized by 3 and 5
- a minor mode is characterized by ♭3 and 5
- a diminished mode is characterized by a ♭5
- we find the basic diatonic scales at the degrees of a major scale: I = ionian, II = dorian, III = phrygian, IV = lydian, V = mixolydian, VI = aeolian and VII = locrian
- the order by harmony of the basic diatonic scales is by fifths: major are IV, I and V, minor are II, VI and III, and diminished is VII
EXERCISES 6
- Sing all of these scales also on the same beginning tone;
- Figure out how to write all of these scales on the same beginning tone;
- Make sure you are eventually able to use all seven basic tones for each.
Harmonic and melodic minor scales
Above we saw the major (also: ionian) and the natural minor (also: aeolian) scales, but there are two more minor scales every musician should be familiar with.
These two scales, harmonic and melodic minor, have each a unique step structure, differing also from that of the basic diatonic scales. To distinguish them more clearly from the natural minor scale, naturals have been added in the following examples on c:

example 16 – harmonic minor
- the step structure is 1 – ½ – 1 – 1 – ½ – 1½ – ½
- the harmonic positions of the tones are 1 – 2 – ♭3 – 4 – 5 – ♭6 – 7
- this scale has a 1½ step, so strictly taken this is not a diatonic scale

example 17 – melodic minor
- the step structure is 1 – ½ – 1 – 1 – 1 – 1 – ½
- the harmonic positions of the tones are 1 – 2 – ♭3 – 4 – 5 – 6 – 7
- consisting of only whole tones and semitones, this is also a diatonic scale
Chromatic scale
The chromatic scale is the scale with only semitone distances, using all 12 tones. Ascending, it is notated with sharps, descending with flats. This facilitates reading, but also represents the musical perception of the functions of the tones mutually:
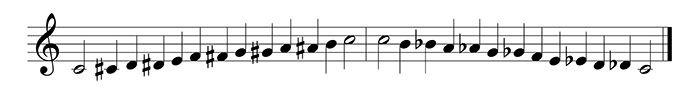
example 18 – ascending and descending chromatic scale
EXERCISES 7
- Sing all of these scales also on different beginning tones;
- Figure out how to write all of these scales on different beginning tones;
- Eventually make sure you are able to use all twelve chromatic tones for each.
goto chapter 4 ► Building blocks of harmony – Intervals
Oscar van Dillen ©2014-16
