 Chapter 4 of the Outline of basic music theory – by Oscar van Dillen ©2011-2020
Chapter 4 of the Outline of basic music theory – by Oscar van Dillen ©2011-2020
The beginner’s learning book can be found at Basic elements of music theory.
Overview of chapters:
Chapter 1: Introduction
Chapter 2: Sound and hearing
Chapter 3: Musical notation
Chapter 4: Basic building blocks of melody and harmony
Chapter 5: Consonance and dissonance
Chapter 6: Circle of fifths and transposition
Chapter 7: Concerning rhythm, melody, harmony and form
Chapter 8: Further study
Scales
Definition of scale
A scale is a collection of tones arranged in a stepwise ascending or descending order, usually spanning one octave, sometimes two.
 The above example in notation is of a theoretical nature, because notation without a clef on the staff does not define the pitches.
The above example in notation is of a theoretical nature, because notation without a clef on the staff does not define the pitches.
This linear representation is one way of looking at a scale, another is the circular representation given in the image below:
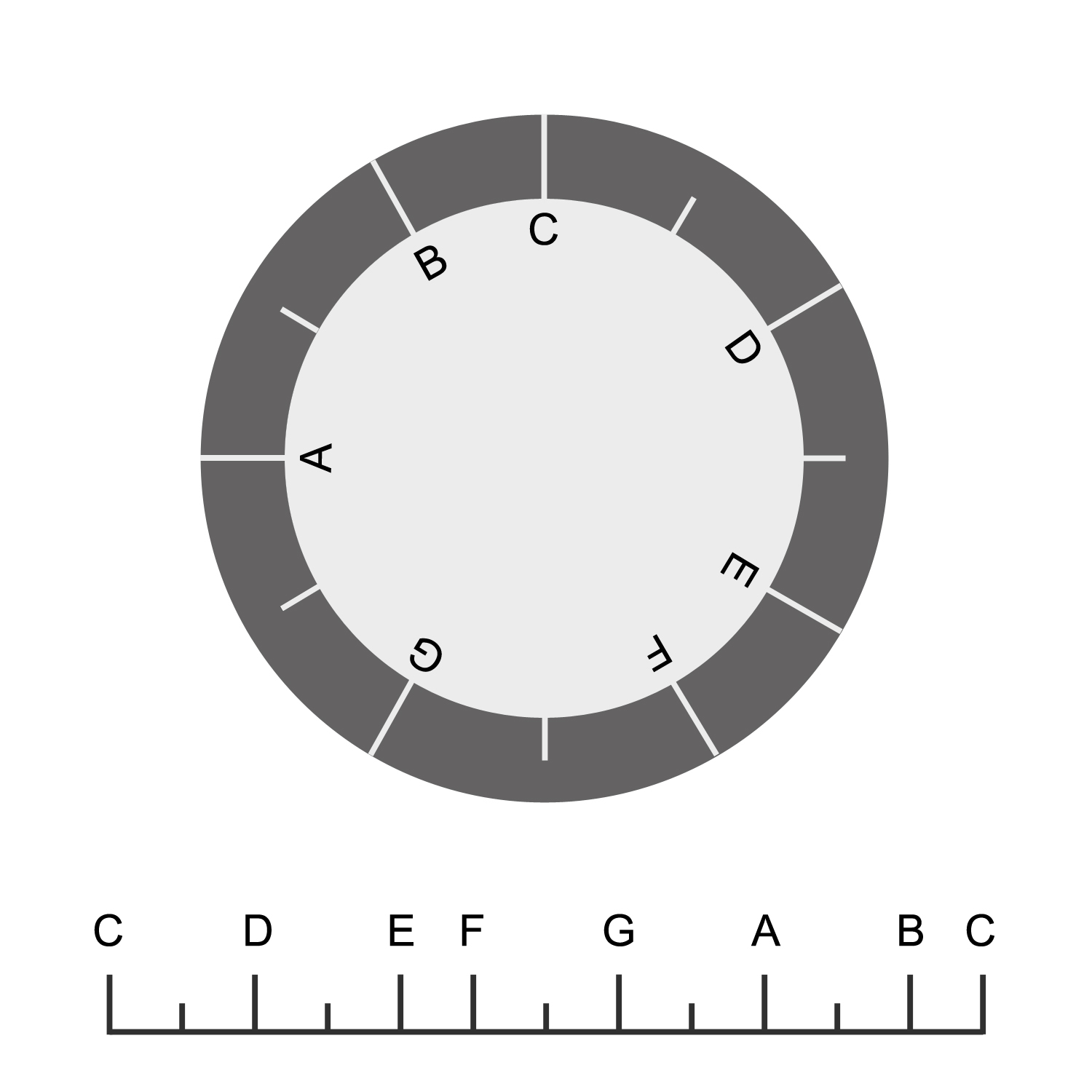
Circular and linear representation of the basic tone scale
Different scales
Different scales can start and end on different tones or tonics, and alteration of tones can be used to achieve an even greater variety of scales. There are numerous scales used throughout the world, sometimes with different ascending and descending scales.
A larger set of scales can be derived from basic major, minor and diminished scales.
Basic major and minor scales
Major scale
The major scale consists of two identical tetrachords (4 note groups), each 1 – 1 – ½ separated by a whole tone, together: 1 1 ½ 1 1 1 ½
 From the major scale the church modes are derived. As a church mode, this scale is called ionian.
From the major scale the church modes are derived. As a church mode, this scale is called ionian.
Natural minor scale
From the major scale the natural minor scale can be derived.
 The natural minor scale is derived from the major scale, which runs from its 6th step: 1 ½ 1 1 ½ 1 1, and it is called aeolian as part of the church modes.
The natural minor scale is derived from the major scale, which runs from its 6th step: 1 ½ 1 1 ½ 1 1, and it is called aeolian as part of the church modes.
Harmonic minor scale
The harmonic minor scale is derived from natural minor by not lowering the seventh step: 1 ½ 1 1 ½ 1½ ½.
 This scale is not a diatonic scale, as there is an augmented second appearing between the 6th and 7th steps.
This scale is not a diatonic scale, as there is an augmented second appearing between the 6th and 7th steps.
From the harmonic minor, the harmonic minor modes can be derived.
Melodic minor scale
The melodic minor scale is derived from both major and minor by combining the lower and upper tetrachords of each, 1 ½ 1 and 1 1 ½ thus running: 1 ½ 1 1 1 1 ½.
 From the melodic minor, the melodic minor modes can be derived.
From the melodic minor, the melodic minor modes can be derived.
Definition of mode
A mode, like a scale, is a collection of tones arranged in a stepwise ascending or descending order, generally spanning one octave.
More than a scale, in musical practice, a mode can have specific melodic requirements for performance, such as a specific order of playing the pitches involved in a makam or raga. Music based on the use of modes is generally called modal music, and though not excluding the use of harmony, this term is generally used in opposition to music “powered” by functional harmony, which is called tonal music.
Church modes
The church modes are modes which are derived from degrees of the major scale.
 “Church modes” is the conventional name for the seven basic theoretical medieval diatonic scales and their related derivatives, which were at the time used in European church music. This modal system was used in medieval music, yet their names are older and derived from ancient Greek music theory.
“Church modes” is the conventional name for the seven basic theoretical medieval diatonic scales and their related derivatives, which were at the time used in European church music. This modal system was used in medieval music, yet their names are older and derived from ancient Greek music theory.
In their basic form the church modes can be notated with only basic tones.
History and use
The church mode system is the predecessor to the Western major-minor diatonic system. The name church modes still refers to their usage in christian Gregorian chant and early polyphony, but since they are a result of a standardization process, they cannot be but a theoretically simplified (and thus highly censored) representation of what was actually sung in early Christendom, which must have had music and scales taken from a much older music, and larger collection of scales, used outside of, not exclusively before the existence of, the christian church. The 7 surviving modes incorporated into this collection are purely diatonical1, and derived from 1 basic scale, they each just start and end on a different tone.
 Since the development of Jazz theory, the church modes, or shorter: “the modes“, have become an integral part of teaching improvisation to jazz musicians. An extraordinary example of a very elaborate system for modal improvisation in jazz is George Russel’s Lydian chromatic concept of tonal organization2. Although the practical value of church modes for modal jazz (mostly with alterations) is undisputed, in fast music (“up tempo“) with fast changes of harmony (“changes“), their actual use remains highly questionable from a theoretical point of view, and is of little practical use.
Since the development of Jazz theory, the church modes, or shorter: “the modes“, have become an integral part of teaching improvisation to jazz musicians. An extraordinary example of a very elaborate system for modal improvisation in jazz is George Russel’s Lydian chromatic concept of tonal organization2. Although the practical value of church modes for modal jazz (mostly with alterations) is undisputed, in fast music (“up tempo“) with fast changes of harmony (“changes“), their actual use remains highly questionable from a theoretical point of view, and is of little practical use.
For pedagogical use these modes are still a wonderful beginners-tool to enhance auditive awareness and develop a sense of melody, interval and harmony, and for developing instrumental improvisation, independent of style; however, they have little practical value for improvising over fast changes.
Different modal systems exist in other traditions, such as the Arabic moqqaam-, the Turkish makam-, the North Indian (often somewhat ethnocentrically called “Hindustani“) thaat-, and South Indian (also called “Carnatic“) melakarta– systems.
Basic notation
The 7 basic modes in basic tones are:
- Ionian – from c to c – c d e f g a b c
- Dorian – from d to d – d e f g a b c d
- Phrygian – from e to e – e f g a b c d e
- Lydian – from f to f – f g a b c d e f
- Mixolydian – from g to g – g a b c d e f g
- Aeolian – from a to a – a b c d e f g a
- Locrian – from b to b – b c d e f g a b
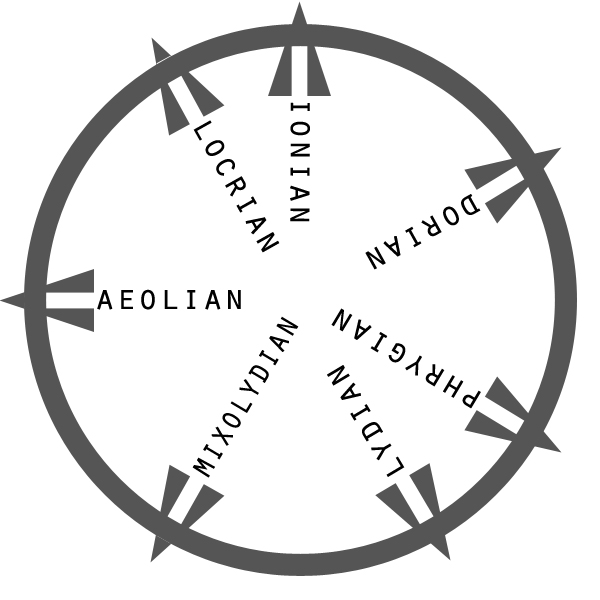
circular representation of the basic diatonic (church) modes
The basic notation of these modes consists of basic tones and can be done without any alterations:

Notation on c
When notating all these modes on c, there appears a different logical order, by the number of alterations needed (as will later be explained, the modes have been transposed here).

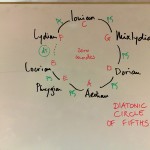 Thus a partial circle of fifths is found with the help of the original tonics: F – C – G – D – A – E – B.
Thus a partial circle of fifths is found with the help of the original tonics: F – C – G – D – A – E – B.
(see also the later chapter on the circle of fifths)
Different modes
 Different modes can start and end on different fundamental tones or tonics, and alteration of tones can be used to achieve an even greater variety of modes. There are numerous modes used throughout the world, sometimes with different ascending and descending scales.
Different modes can start and end on different fundamental tones or tonics, and alteration of tones can be used to achieve an even greater variety of modes. There are numerous modes used throughout the world, sometimes with different ascending and descending scales.
(see also the headings on minor harmonic and minor melodic modes in the music theory reference)
Intervals
Definition of interval
An interval in music is the sound of exactly two tones sounding together, or one after the other.
All intervals can be measured by the number of diatonic steps and by their semitone distances. More technically, an interval can also be described as a frequency ratio relationship between two stable vibrations. All intervals can also occur on (above or below) all tones.
Many different tunings and hence intervals have been developed and used in various traditions3, this Outline of basic music theory treats the internationally customary tuning in Equal Temperament4.
One sound
The sounding together of two tones creates a blending of the two into a new, specific sound, is called the interval. Within the sound of each interval, partial tones can be perceived, emerging from the interaction of frequencies as sum- and difference tones. Each interval thus consists of far more than just the two tones played or performed: it is a complex sound which is at first perceived as a whole.
Basic intervals
Due to notation, intervals are named by the distance between the two basic tones they consist of.
When the lowest tone is counted as 1, the name of the interval follows from counting in diatonic steps upwards (although reversing this direction gives the same result):

Wide intervals
Wider than the octave, music theory describes larger intervals. Though similar, the sound of these is also quite different from that of their related narrower intervals.
 The similarity with the narrower basic intervals lies in the fact, that both contain the same harmonic content: the same pitches of tones. Yet the actual sound of these wide intervals, e.g. with regard to consonance and dissonance, is at the same time so different, that they can be considered as independent musical entities as well: these are intervals in their own right, and not mere octave transpositions. It is for this very reason that I strongly oppose using the term compound intervals, because also these have their own sound qualities, each one sound, not “compound” therefore.
The similarity with the narrower basic intervals lies in the fact, that both contain the same harmonic content: the same pitches of tones. Yet the actual sound of these wide intervals, e.g. with regard to consonance and dissonance, is at the same time so different, that they can be considered as independent musical entities as well: these are intervals in their own right, and not mere octave transpositions. It is for this very reason that I strongly oppose using the term compound intervals, because also these have their own sound qualities, each one sound, not “compound” therefore.
Perception of the interval
The unique sound of each interval can be immediately recognized by hearing, making it in fact a truly fundamental element of all music.
When listening to two simultaneous tones, their pitches and frequencies mix and react, creating even more tones sounding together: interference tones. This complex of tones becomes one comprehensive sound, and the individual pitches become acoustically more or less absorbed into the human perception of the single interval: the interval itself is in fact perceived as louder than the individual tones it consists of. It is human perception which “summarizes” the tones into the single interval, but it has good acoustic reasons to do so. Thus the interval is equally the basic prerequisite for all melody as it is for harmony.
Basic intervals from c
The basic intervals using only basic tones from c are shown below.
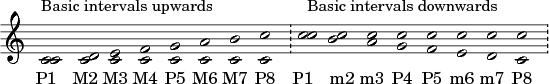 The second series consists in fact of inversions of the first, in reverse order.
The second series consists in fact of inversions of the first, in reverse order.
Full names of the intervals
A full name of an interval consists of the quality plus the distance, such as minor second (m2), perfect fifth (P5), or augmented sixth (A6) etc.
Each interval thus has a “first name” and a “last name”.
For the purpose of shorter and easier writing the names of the intervals are abbreviated in the following way: the intervals are represented by numbers, their qualities by preceding letters.
Summary of the abbreviations:
Qualities: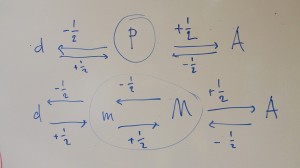
- M = Major
- m = minor
- P = Perfect
- A = Augmented
- d = diminished
Distances:
- 1 = unison
- 2 = second
- 3 = third
- 4 = fourth
- 5 = fifth
- 6 = sixth
- 7 = seventh
- 8 = octave
The whiteboard image shows the semitone relationships between the qualities of intervals:
- perfect are the unison, fourth, fifth and octave plus wider versions of these;5
- major is larger than minor;
- augmented is larger than major or perfect;
- diminished is smaller than minor or perfect.
Finally, even double diminished and double augmented intervals are hypothetically possible, but of no practical value at all.
The table below thus lists all possible basic intervals, including augmented and diminished intervals. Below the table, all these are also presented in notation, with c as reference tone (remember, all intervals can occur on -above or below- all tones!).
| diminished | minor | Perfect | Major | Augmented | |
| unisons | d1 | P1 | A1 | ||
| seconds | d2 | m2 | M2 | A2 | |
| thirds | d3 | m3 | M3 | A3 | |
| fourths | d4 | P4 | A4 | ||
| fifths | d5 | P5 | A5 | ||
| sixths | d6 | m6 | M6 | A6 | |
| sevenths | d7 | m7 | M7 | A7 | |
| octaves | d8 | P8 | A8 |
In this table the empty places occur because these intervals do not exist (e.g. there is no perfect third, no major fifth etc.).

Intervals in order of chromatic size
The table below lists all possible basic intervals in order of number of semitones, these are also presented in notation with their enharmonic equivalents, with c as reference tone (remember, all intervals can occur on -above or below- all tones!).
| size | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| intvl | d1 | P1, d2 | m2, A1 | M2, d3 | m3, A2 | M3, d4 | P4, A3 | A4, d5 | P5, d6 | m6, A5 | M6, d7 | m7, A6 | M7, d8 | P8, A7 | A8 |

Enharmonic equivalence
The possibility of writing one and the same sound with two different diatonic spellings is called enharmonic equivalence; such two intervals are enharmonically the same. When listened to separately, the number of semitones will determine the sound, and in ear-training usually the simpler spelling is heard, interpreted and given. Within a certain musical context however, more complex phenomena may occur, requiring specific writing, spelling and nomenclature, giving prevalence to one of the two possibilities for contextual reasons.
In one case, a special name was assigned to such a pair of enharmonically equivalent intervals: the name tritone can be used to designate both the augmented fourth and the diminished fifth; this unique interval acoustically equals its own inversion. The name was derived from the fact that this interval equals exactly three whole tone distances (six semitones).
Inversions of the intervals
The inversions describe close relationships between intervals in pairs: an interval and its inversion use the same notes, but in different order or position. The two inversions together span a perfect octave, 12 semitones, thus the inversion of a Major third is a minor sixth, calculated as M3 (4 semitones) and m6 (8 semitones), together 4 + 8 = 12 semitones (P8).
The close relationship between inversions can be clearly heard, as well as the fundamental difference in sound. No interval should be mixed up with its inversion, they are not identical, nor is one derived from the other6.
The inversions are below presented in notation, with c as reference tone (remember, all intervals can occur on -above or below- all tones!).
 The inversion of a perfect interval is always a perfect interval, the inversion of a major interval always a minor interval, the inversion of a diminished interval always an augmented interval, and all vice versa as well. The inversion of a second is a seventh, of a third a sixth, of a fourth a fifth, and vice versa. The tritone is the only interval which is enharmonically the same as its inversion, such as can be heard by playing the above example.
The inversion of a perfect interval is always a perfect interval, the inversion of a major interval always a minor interval, the inversion of a diminished interval always an augmented interval, and all vice versa as well. The inversion of a second is a seventh, of a third a sixth, of a fourth a fifth, and vice versa. The tritone is the only interval which is enharmonically the same as its inversion, such as can be heard by playing the above example.

easy inversion finder
The table above is to help quickly find the names of the inversions by qualities and distances.7
Triads
Definition of triad
A triad is a special type of chord which consists of 3 different tones, in consecutive thirds.
The triad thus consists of a minimum of three intervals: 2 thirds and 1 fifth, or their respective inversions.
Basic notation
The basic notation of a triad, is by virtually taking tones 1, 3 and 5 of a scale and writing them together.
The examples below use the basic tones only.
Basic scale and triad of c:
Basic scale and triad of d:
Basic scale and triad of e:
Basic scale and triad of f:
Basic scale and triad of g:
Basic scale and triad of a:
Basic scale and triad of b:
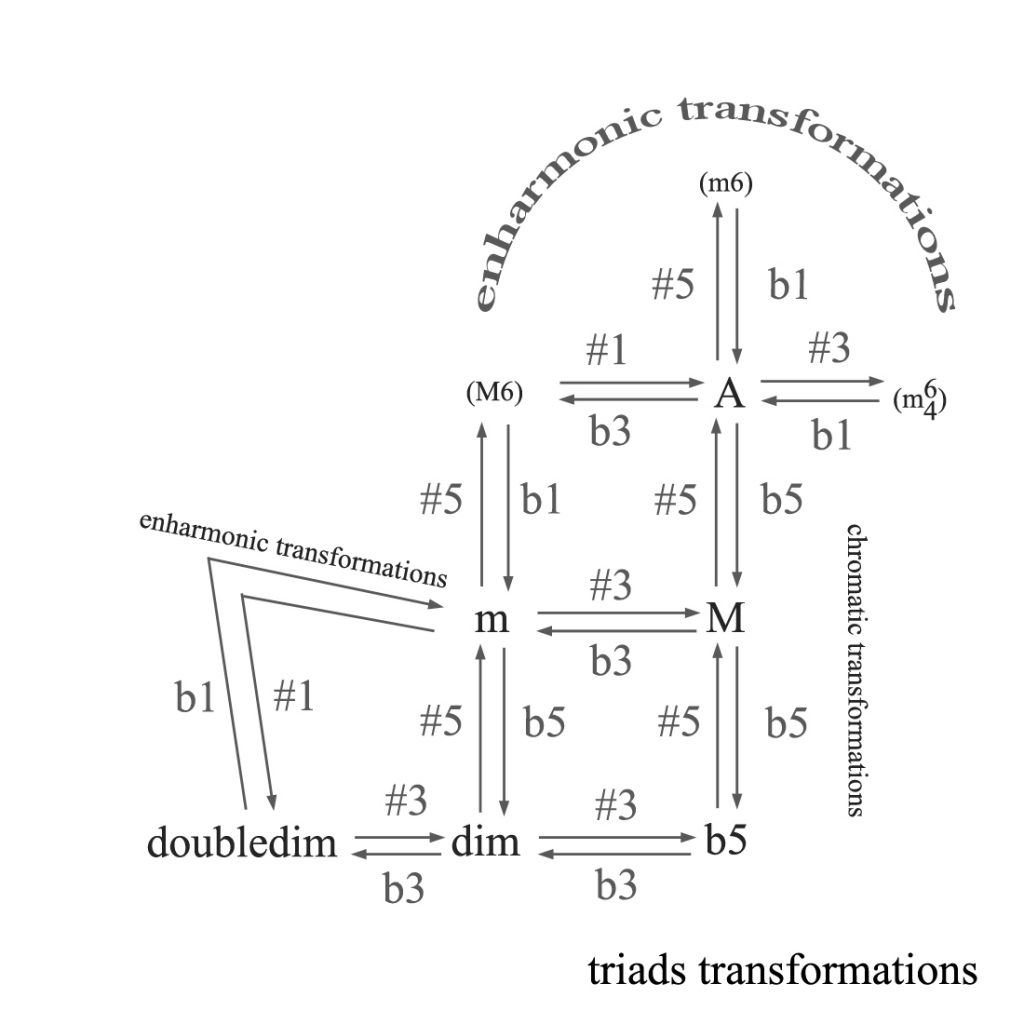
Types of triads
Consisting of 2 thirds and one fifth, the thirds can be major or minor, and the fifth can be perfect, diminished or augmented, there are 6 types of triads.
- Major triad: consisting of a major third, a minor third and a perfect fifth;
- Minor triad: consisting of a minor third, a major third and a perfect fifth;
- Augmented triad: consisting of a major third, a major third and an augmented fifth;
- Diminished triad: consisting of a minor third, a minor third and a diminished fifth;
- Flat 5 triad: consisting of a major third, a diminished third and a diminished fifth;
- Double Diminished triad: consisting of a diminished third, a major third and a diminished fifth.
These triads can occur on any tone, the examples below are the 6 triads of c (alterations are needed to obtain the tones):

Symbols for triads
For most music in which improvising plays an important role, symbols are used for triads and chords.
There is no unity in the systems used for these symbols, as different symbols occur in different books.
Below is a table summarizing the most commonly used chord-symbols for triads:

Inversions of triads
A triad is still considered to be the same triad when the 3 tones it consists of are presented in another position than the basic 1-3-5 described so far. There are three basic positions for a triad:
- The 1 is the lowest tone, this is called root position, short: root
- The 3 is the lowest tone, this is called first inversion or sixth position, short: 6
- The 5 is the lowest tone, this is called second inversion or six-four position, short: 6-4
The acoustic properties are different, yet these positions can be perceived as derived from one basic structure: the triad. This perception evolved by the end of the 15th century in Europe, and the triads (and their inversions) quickly entered Western classical music to dominate it for centuries to come, at the cost of the polyphony which prevailed before. Harmony thus replaced melody as the structuring principle of musical logic.
The examples below are the positions of the triads of c:
 The names of the inversions are derived from the intervallic structure: the inversions of the thirds become sixths (major, minor or augmented), and the inversions of the fifths become fourths (perfect, augmented or diminished).
The names of the inversions are derived from the intervallic structure: the inversions of the thirds become sixths (major, minor or augmented), and the inversions of the fifths become fourths (perfect, augmented or diminished).
Other positions of triads
Any chord with more than just three tones, but consisting of just three tones making up a triad, is also perceived as, and considered to be, a triad. In this way, triads can be performed with more pitches, yet three basic tones only, as is the case in many compositions for piano, band, choir, ensemble or orchestra.
Other designations for positions of triads are:
- closed position – short CP, when no triad-tones fit between the tones played, the position of the lowest tone, the bass, is disregarded in this respect
- open position – short OP, when exactly one triad tone would fit between the tones played, the position of the lowest tone, the bass, is disregarded in this respect
- mixed position – short MP, when the position has a mix of “open” and “closed” interval positions; the position of the lowest tone, the bass, is disregarded in this respect
- octave position – short 8P, when the highest tone played is the 1
- third position – short 3P, when the highest tone played is the 3
- fifth position – short 5P, when the highest tone played is the 5
Some examples, demonstrating these positions of the triad of c-major, for piano:

Use of triads
Any scale or mode can be harmonized by forming triads on its steps, as such these triads (or, when expanded: seventh chords) can be called degrees.
The harmony thus obtained is proper to that particular scale itself and can be modal or tonal, depending on its use.
Mutual sound relationships and possible transformations of triads
As all triads are closely related sounds, changing just one tone usually results in another triad. These mutual sound relations and transformations are given in the image below:
Seventh chords
Definition of seventh chord
A ‘seventh chord is a special type of chord which consists of 4 different tones, in consecutive thirds.
The seventh chord thus consists of a minimum of six intervals: 3 thirds, 2 fifths and 1 seventh, or their respective inversions.
A seventh chord can be regarded as en expanded triad; each seventh chord itself consists of 2 triads.
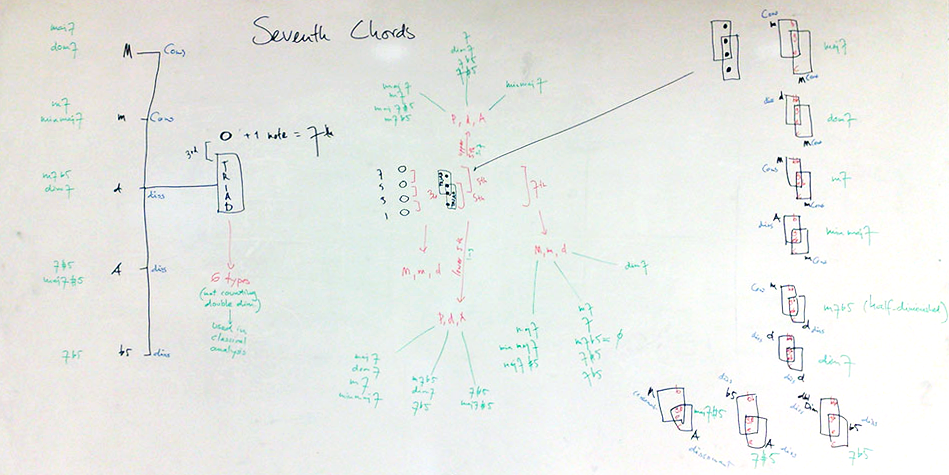
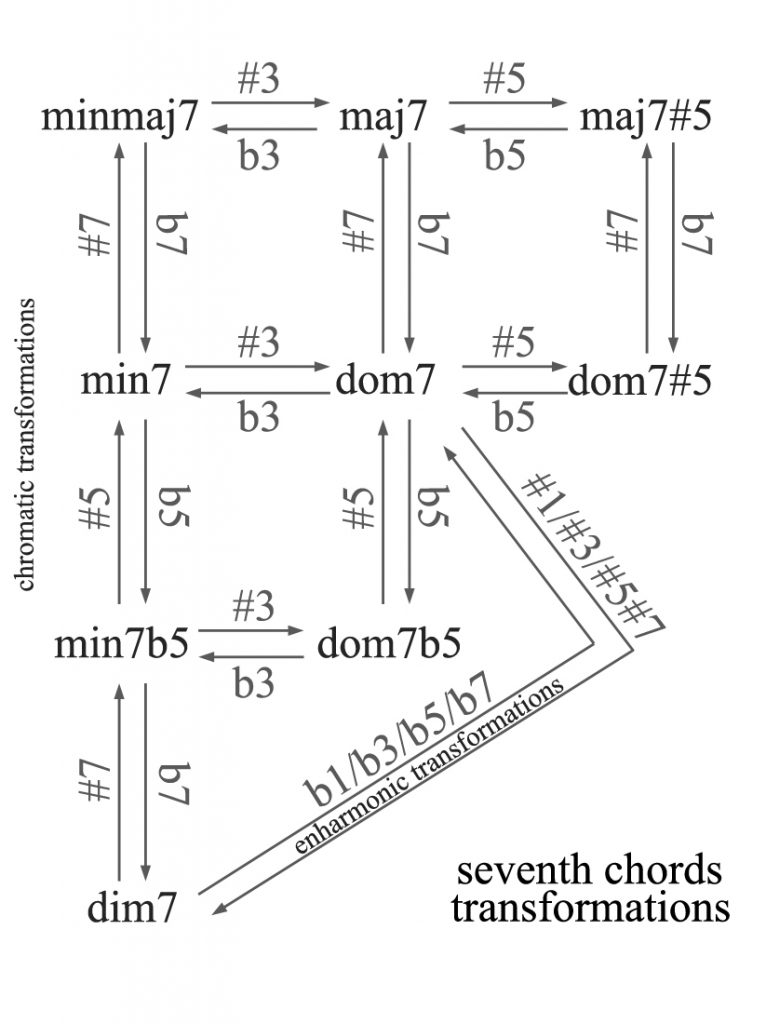
constructions and transformations of seventh chords
The relationships of all types of seventh chords with their constituent triads and intervals are shown in the whiteboard picture above.
Basic notation
The basic notation of a seventh chord, is by virtually taking tones 1, 3, 5 and 7 of a scale and writing them together, sounding as one.
The example below uses the basic tones only.

Types of seventh chords
Consisting of 3 thirds, 2 fifths and 1 seventh, the thirds can be major, minor or diminished, fifths can be perfect, diminished or augmented, the sevenths can be major, minor or diminished. There are no seventh chords which contain an augmented third, as the enharmonic equivalence of this interval, the perfect fourth, is such a strong consonant that its top note would acoustically assume the position of the root of the whole chord, thus leading to the perception of an extended triad. Thus the number of possible seventh chords is limited to just 11:
- Major seventh chord: consisting of a major third, a minor third, a major third, two perfect fifths and a major seventh
- Dominant seventh chord: consisting of a major third, a minor third, a minor third; one perfect fifth, one diminished fifth and a minor seventh
- Minor seventh chord: consisting of a minor third, a major third, a minor third; two perfect fifths and a minor seventh (enharmonically equivalent to a Major triad with added 6 in third inversion)
- Minor major seventh chord: consisting of a minor third, a major third, a major third; one perfect fifth, one augmented fifth and a major seventh
- Half diminished chord: consisting of two minor thirds, a major third; one diminished fifth, a perfect fifth and a minor seventh (enharmonically equivalent to a Minor triad with added 6 in third inversion)
- Diminished seventh chord: consisting of three minor thirds; two diminished fifth and a diminished seventh (enharmonically equivalent to itself in all inversions)
- Augmented seventh chord: consisting of two major thirds, a minor third; an augmented fifth, a perfect fifth and a major seventh
- Augmented dominant seventh chord: consisting of two major thirds, a diminished third; an augmented fifth, a diminished fifth and a minor seventh
- Flat 5 dominant seventh chord: consisting of a major third, a diminished third, a major third; two diminished fifths and a minor seventh (enharmonically equivalent to itself in second inversion)
- Double diminished minor seventh chord: consisting of a diminished third, a major third, a major third, a diminished fifth, an augmented fifth and a minor seventh (enharmonically equivalent to an Augmented dominant in third inversion)
- Double diminished seventh chord: consisting of a diminished third, a major third, a minor third, a diminished fifth, a perfect fifth and a diminished seventh (enharmonically equivalent to a Dominant seventh in third inversion)
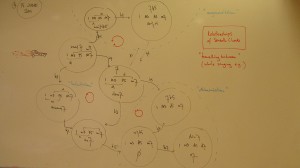 The whiteboard image on the right shows the relative mutual proximity and similarity of the 9 basic seventh chords.
The whiteboard image on the right shows the relative mutual proximity and similarity of the 9 basic seventh chords.
The arrows indicate how an alteration of one chord tone will change the chord into a neighbouring, different, but closely related, related seventh chord.
All seventh chords can occur on any tone, the notated example below shows all 11 theoretically possible seventh chords of c (alterations are needed to obtain the correct tones). In practice however, only 9 seventh chords have actual chord-symbols: the last two seventh chords have no chord-symbol of themselves. These two would rather be notated as third inversions, slash chords of d (D7#5/C and D7/C, as notated in small black notes), of which they are enharmonic equivalents:

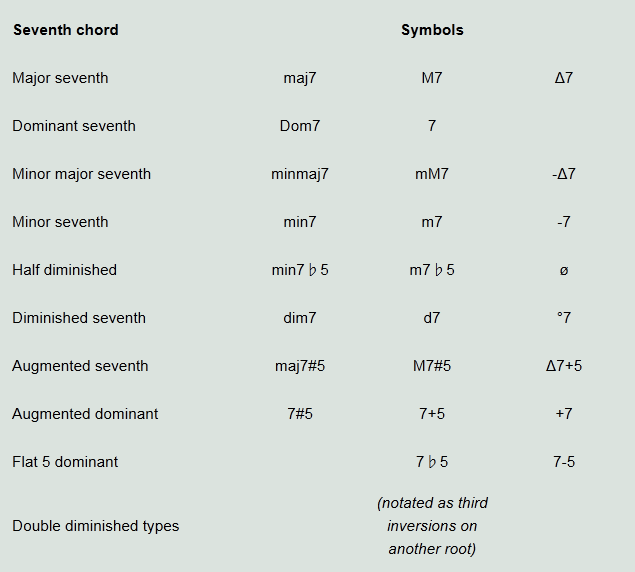
Symbols for seventh chords
For most music in which improvisation plays an important role, symbols are used for seventh chords.
There is no unity in the systems used for these symbols, as different symbols occur in different books.
Below is a table summarizing the most commonly used chord-symbols for seventh chords:
Inversions of seventh chords
A seventh chord is still considered to be the same seventh chord when the 4 tones it consists of are presented in another position than the basic 1-3-5-7 described so far. There are four basic positions for a seventh chord:
- The 1 is the lowest tone, this is called root position, short: 7
- The 3 is the lowest tone, this is called first inversion or six-five position, short: 6-5
- The 5 is the lowest tone, this is called second inversion or four-three position, short: 4-3
- The 7 is the lowest tone. this is called third inversion or second position, short: 2
The acoustic properties are different, yet these positions can be perceived as derived from one basic structure: the seventh chord.
The examples below are basic tone positions of seventh chords twice, both of c and on c:

The names of the inversions are derived from the intervallic structure: the inversions of the thirds become sixths (major, minor or augmented), the inversions of the fifths become fourths (perfect, augmented or diminished) and the inversions of the sevenths become seconds (major, minor or augmented).
 The whiteboard image on the right shows a full table of the nine seventh chords that have chord symbols, in all inversions on c (and here not of c, as only the root positions are C chords!).
The whiteboard image on the right shows a full table of the nine seventh chords that have chord symbols, in all inversions on c (and here not of c, as only the root positions are C chords!).
Use of seventh chords
Any scale or mode can be harmonized by forming seventh chords on all its steps. These seventh chords are then called degrees.
The harmony thus obtained is proper to that particular scale itself and can be modal or tonal, depending on its use.
Mutual sound relationships and possible transformations of seventh chords
As all seventh chords are closely related sounds, changing just one tone usually results in another seventh chord. These mutual sound relations and transformations are given in the image below:
Oscar van Dillen ©2011-2020
goto chapter 5 ► Consonance and dissonance
Footnotes
- diatonical means: consisting of whole and half tone (semitone) distances only, not containing any larger intervals such as augmented seconds nor any thirds. ↩
- The Lydian chromatic concept of tonal organization described on www.georgerussell.com ↩
- List of pitch intervals including other tuning systems, on Wikipedia (with sound examples) ↩
- Equal temperament explained on Wikipedia ↩
- seconds, thirds, sixths and sevenths, plus the wider versions of these, are never perfect but either major or minor ↩
- Rameau, Treatise on Harmony (1722) ↩
- More information on intervals can be found in the Reference Guide ↩
